五个月前，美国的激光干涉引力波观测站 LIGO 记录下这片时空里泛起的一丝波澜。这正是爱因斯坦广义相对论中的引力波。

LOSC 上有一篇详实的数据处理教程。正所谓“绝知此事需躬行”，这里我们用 Mathematica 复现教程里的结果。

1. 准备数据

下载两个观测站上采样率为 4096sps 的两组数据。

2. 初步分析

数据格式为 HDF5，Mathematica 可以直接读取。

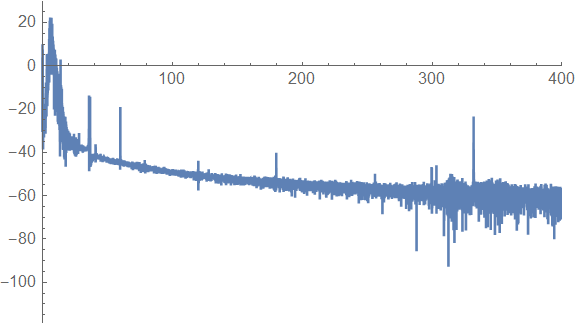
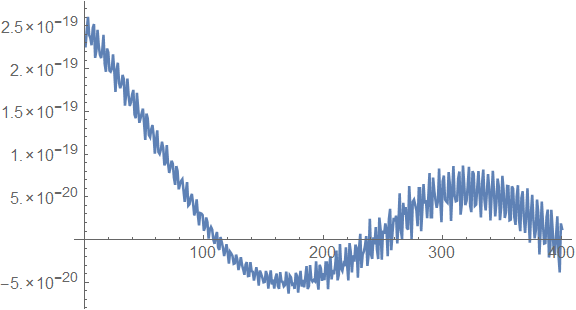
从 H-H1 站数据的频谱图上可以看出，原始数据里含有丰富的低频分量，以及多个很强的系统固有的谐波干扰。从时域波形上也能大致看出类似现象。

Fs = 4096;
hh1 = Import[
   "H-H1_LOSC_4_V1-1126259446-32.hdf5", {"Datasets", "/strain/Strain"}];
Periodogram[hh1 10^18, SampleRate -> 4*1024, PlotRange -> { {0, 400}, All}]
ListPlot[hh1[[;; 400]], Joined -> True, PlotRange -> All]

freq domain

time domain

3. 带通滤波

有效数据的频率范围大概在 40Hz 到 300Hz 之间，我们在 Mathematica 里设计一个 500 阶 FIR 带通滤波器，通带范围可以稍微再小一点：

StrainBPF[data_, samplerate_] :=
  BandpassFilter[data, {40, 260} 2 \[Pi]/samplerate, 500];

从上面的频谱图上看到，低频分量比我们关注的频段强 60dB 左右，我们的这个滤波器阻带衰减无法把低频分量完全滤除。为此，可以把 2 到 3 个相同的带通滤波器串联使用。

4. 陷波

IIR 陷波器可以很直观地设计出来：在共振点上设置一个零点，然后在零点附近设置一个极点。陷波器是因果稳定的，所有极点要在单位圆内；我们考虑实信号，所以把这对零极点的共轭对称点也分别设置为零极点，如下图所示。

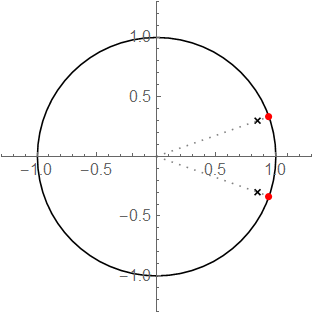
trap filter

陷波器设计如下：

code

考查经过 3 次 BPF 后的数据，可以发现需要在这些频率上进行陷波：{35.9, 36.7, 40.97, 60.00, 120, 180}。

5. 综上

最后，将上面的带通滤波及陷波组合起来，引力波的波形就魔术般地呈现在我们眼前。

tevent = 1126259462.422; (* Mon Sep 14 09:50:45 GMT 2015*)
tstart = Import[
   "H-H1_LOSC_4_V1-1126259446-32.hdf5", {"Datasets", "/meta/GPSstart"}];
SelData[data_, {start_, stop_}] :=
   data[[Round[(tevent - tstart + start) Fs] ;; Round[(tevent - tstart + stop) Fs]]]
all = Reap[Fold[
     With[{r = #2[#1]}, Sow@SelData[r, {-0.2, 0.3}]; r] &,
     hh1,
     {Identity, StrainBPF[#, Fs] &, StrainBPF[#, Fs] &, StrainBPF[#, Fs] &}
      ~Join~
      (Function[{data}, WaveTrap[data, #, Fs]] & /@ {35.9, 36.7, 40.97, 60.00, 120, 180})
     ];];
labeled = MapThread[{#1, #2} &,
   {all[[2, 1]], {"origin", "bpf", "bpf \[Times] 2", "bpf \[Times] 3"}
     ~Join~
     FoldList[#1 <> ", " <> ToString[#2] &,
      "bpf \[Times] 3 + trap 35.9", {36.7, 40.97, 60.00, 120, 180}]}];
l = ListPlot[#[[1]], Joined -> True, PlotRange -> All,
     PlotLabel -> Style[Framed@#[[2]], 16, Blue, Background -> Lighter[Yellow]]] & /@ labeled;
ListAnimate[l]

demo

这段引力波在频域上的“啁啾”芳容也同时展现：

demo

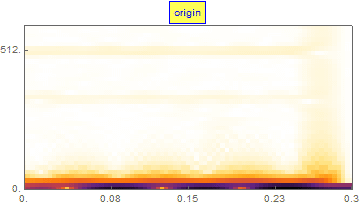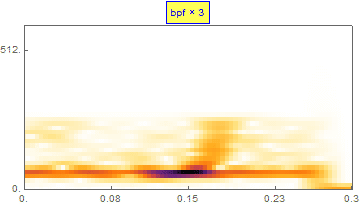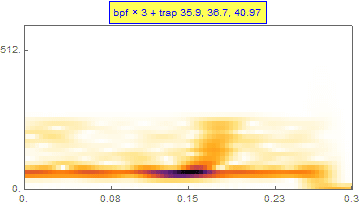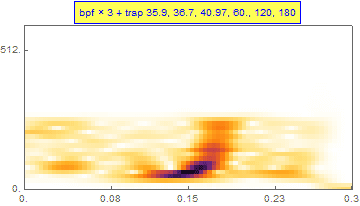
6. 频域处理

像此类数据，绝大多数都可视为噪声，极偶然的情况下，才能接收到零星的数据，而且一旦接收到，那就是个“大新闻”。所以，这样的数据可以先白化，使频谱变平缓，噪声基本变成“白噪声”。

这里的白化处理比较简单，只要先估计出一个相对比较平滑的频谱，用其幅度去除频谱即可。

Options[WelchPSD] = {"WindowFunction" -> HannWindow, "Overlap" -> 0};
WelchPSD[data_, len_, OptionsPattern[]] :=
  With[{w =
     OptionValue[
       "WindowFunction"] /@ (4/len Most@Range[-len/2, len/2]),
    ls = Partition[data, len, len - OptionValue["Overlap"]]},
   Total[Abs[#]^2 & /@ Fourier[w #] & /@ ls]/Length@ls];
FFTFreq[fs_, n_] :=
  With[{l = # fs/n & /@ Range[0, Quotient[n, 2]]},
   l~Join~-Reverse@l[[2 ;; Mod[n, 2] - 2]]];

(* 先用较短的长度 psdlen 估计功率谱，以内插后的幅值去做白化 *)
Whiten[data_, fs_, psdlen_] := With[
   {interp =
     Interpolation@
      MapThread[List, {FFTFreq[fs, psdlen], WelchPSD[data, psdlen]}]},
   InverseFourier@(Fourier@data/
      Sqrt[interp /@ FFTFreq[fs, Length@data]])
   ];

白化之后，再看“那个信号”前后 5 秒的频谱，一条可爱的小尾巴显露出来：

gw after whitening

白化一来消除了强谐波干扰，二来低频部分也被压了下来。现在只用一个带通滤波器就可以把引力波检出来了：

ListPlot[StrainBPF[SelData[Re@Whiten[hh1, Fs, Fs], {-0.1, 0.05}], Fs],
  Joined -> True, PlotRange -> All]