转眼高中毕业十五年,恍惚之间物理知识已经忘得差不多了,但是一道物理题却一直萦绕心头,历久弥新。
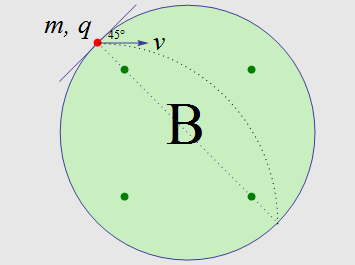
单位圆区域内有如图的匀强磁场。现有一质量为 $m$,所带电量为 $q$ 的带正电粒子沿垂直于磁场的方向以速度 $v$ 射入该磁场, $v$ 与入射点切线夹角为 $45^{\circ}$。磁场强度不同,粒子在磁场中的运动轨迹不同。求能使粒子在磁场经过的 距离 路程最长的磁场强度 $B$。
参考答案
弦越长,所对的短弧越长,所以最长的运动轨迹所对的弦恰好为单位圆的直径,如上图虚线所示。场强 $B$ 的计算略。
十五年后的解答
这道题当时没做出来,但对参考答案甚是怀疑,直观感觉如果运动轨迹“更弯”一点,可能弧长更长。已经记不清具体做了哪些计算,似乎算过轨迹半径为 1 的情况,可以确信参考答案错了。我还充分利用仅有的一点微积分知识,用了很多节晚自习的时间苦苦计算,最后也没有得到答案。
又快高考了,也是时候跟这个问题做个了断了,三行 Mathamatica 代码:
\[{In:}\ \text{sol}=\text{Solve}\left[\left\{x^2+y^2=1^2,\left(\left(r-\frac{\sqrt{2}}{2}\right)+y\right)^2 +\left(x+\frac{\sqrt{2}}{2}\right)^2=r^2\right\},\{x,y\}\right]\] \[{Out:}\ \left\{\left\{x\to -\frac{1}{\sqrt{2}},y\to \frac{1}{\sqrt{2}}\right\},\left\{x\to \frac{5 r^2}{\sqrt{2} r^2-2 r+\sqrt{2}}-\frac{3 \sqrt{2} r}{\sqrt{2} r^2-2 r+\sqrt{2}}+\frac{1}{\sqrt{2} r^2-2 r+\sqrt{2}}-\frac{\sqrt{2} r^3}{\sqrt{2} r^2-2 r+\sqrt{2}}+r-\sqrt{2},y\to \frac{r^2-2 \sqrt{2} r+1}{\sqrt{2} r^2-2 r+\sqrt{2}}\right\}\right\}\] \[{In:}\ \text{ArcTan2}(\text{x$\_$},\text{y$\_$})\text{:=}\text{With}\left[\left\{a=\tan ^{-1}(x,y)\right\},\text{If}\left[a>\frac{\pi }{2},a-2 \pi ,a\right]\right];\] \[{In:}\ \text{NMaximize}\left[r \left(\frac{\pi }{2}-\text{ArcTan2}\left(x+\frac{\sqrt{2}}{2},\left(r-\frac{\sqrt{2}}{2}\right)+y\right)\right)\text{/.}\, \text{Last}[\text{sol}],r\right]\]${Out:}\ {2.35687,{r\to 0.977138}}$
这里,Mathamatica 9.0 没能得出解析解,以数值近似解代替。
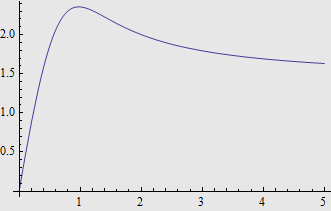
最后,粒子不同轨迹半径与所经 距离 路程的对应关系如下: