压缩感知(Compressed Sensing),也称稀疏采样(Sparse Sampling),是一种求解欠定线性系统以重建信号的方法。
压缩感知
考虑一个欠定系统$y = A x$,我们无法解出$x$,或者说有无数的解,却不知道该如何选择。假如$x$是稀疏的,即其中多数元素都为 0,那么不妨遵照奥卡姆剃刀法则,取 0-范数最小的做为最优解:
\[\underset x {min} \|x\|_0, \ \ \ \ \ subject \ to \ \ y = Ax\]这个优化问题运算量大,于是 Donoho 等提出可以以 1-范数代之:
\[\underset x {min} \|x\|_1, \ \ \ \ \ subject \ to \ \ y = Ax\]现在这个问题可用线性规划方法进行逼近。
考虑一个更实用的带加性噪声的欠定系统$y = A x + n$,$A \in \mathbb{R}^{n \times m} $。Emmanuel Candès, Terence Tao提出“均匀不确定性原理”(Uniform Uncertainty Principle),当$A$具有受限等距特性时,可以稳定且准确地恢复出$x$。
任取$T \subset {1,\ 2,\ \dots,\ n}$,引入记号$A_T$表示由$T$中元素指定的各列组成的子矩阵。Emmanuel Candès, Terence Tao 等定义$A$的$S-$受限等距常数$\delta_S$为:
\[\delta_S = \underset \delta {min} (1-\delta)\|c\|_2^2 \leq \|A_T \ c\|_2^2 \leq (1+\delta)\|c\|_2^2, \ \forall |T| \leq S,\ \forall (C_j)_{j \in T}\]这要求抽取$A$任意不多于$S$列近似正交。
Emmanuel Candès, Terence Tao 中证明如果$\delta_{3 S} + 3 \delta_{4 S} < 2$,那么对于任意非 0 元素个数不大于$S$的$x$,下式给出的解:
\[(P1) \ \ \ \hat x = \underset x {min} \|x\|_1, \ \ \ \ \ subject \ to \ \ \|y - Ax\|_2 \leq \epsilon\]是稳定、准确的:
\[\|\hat x - x\|_2 \leq C_S \ \epsilon\]这里$\epsilon$是噪声的功率的一个上限,$|n|2 \leq \epsilon$,常数$C_S$可能只依赖于$\delta{4 S}$。
注意,上文里的$A$各列的模都已经过归一化处理。
$(P1)$是二阶凸优化的简单特例,有现成的工具包可用,比如 OpenOPT。
同频多小区信道估计
压缩感知在成像领域应用前景非常广阔,这里讨论一下在 TD-SCDMA 同频信道估计上的应用。TD-SCDMA 在利用联合检测解调信号前需要利用中间码(midamble)做信道估计。Midamble 采用了循环前缀,通过简单的 FFT/IFFT 即可实现信道估计的快速计算。
对于存在功率不可忽略的同频小区的情况,上述算法得到的结果会包含严重的同频干扰。现在大多采用串行干扰抵消算法:
- 用 FFT/IFFT 得到各小区的(初始)信道估计
- 从各小区的信道估计选出最强的抽头
- 计算并抵消该抽头对其它小区的干扰
- 标记该抽头使其不再参与后续强抽头的选取
重复步骤 2~4 至一定次数,得到最终的信道估计。
信道冲激响应中的有效插头稀疏分布,可以使用压缩感知做信道估计,至于构造出的矩阵$A$是否满足均匀不确定性原理, 我们这里暂不做详细计算。
假设可能接收到自来$n$个同频小区的信号,
\[y= (\sum_{i=1}^n M_i h_i) + n=\begin{bmatrix} M_1 & \dots & M_n\end{bmatrix} \begin{bmatrix}h_1 \\ \vdots \\h_n \end{bmatrix} + n= \mathbf{M} \mathbf{h}+ n\]鉴于 SOCP 工具只支持实数域,可以将上式拆成实部、虚部两个部分,
\[\mathbf{M}'=\begin{bmatrix}Re\{\mathbf{M}\} & -Im\{\mathbf{M}\} \\ Im\{\mathbf{M}\} & Re\{\mathbf{M}\} \end{bmatrix},\ \mathbf{h}'=\begin{bmatrix}Re\{\mathbf{h}\} \\ Im\{\mathbf{h}\} \end{bmatrix}\]最后还需要将$\underset x {min} |x|_1$转化为 OpenOPT 需要的$\underset \alpha {min} f^T \alpha$,
\[\alpha = \begin{pmatrix}u\\v\end{pmatrix},\ f= \begin{pmatrix}1 \\ \vdots \\ 1\end{pmatrix}, \ x=u-v,\ u > 0, \ v>0\]实验显示,压缩感知给出的信道估计远远优于串行干扰抵消算法,例如下图;当然,计算量也远大于串行干扰抵消:
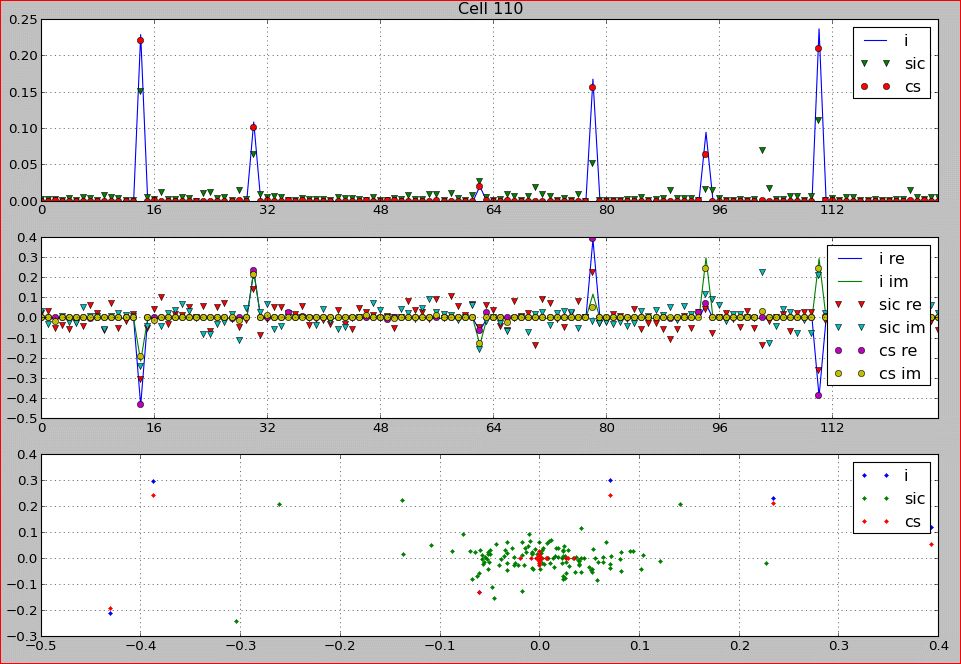
最上面为理想信道估计(i)和串行干扰抵消(sic)、压缩感知(sc)的结果在各抽头上的功率对比,中间为各抽头实虚部的对比,最下为各抽头星座图的对比。