本文就从 2011 年第 1 期开始到 2013 年第 12 期止共 36 期的摇号数据做了分析。主要内容包括:
- 当前摇号机制的不公平
- 社会行为中的欠阻尼振动现象
- “孤独的编码”探奇
1. 背景:摇号的实现
每位申请人对应唯一一个申请编码,每月将所有满足要求的申请人编码从小到大依次排列,并用 1, 2, … 做为摇号基数编码。(注:简便起见,本文对于从 2014 年第 1 期开始的所谓加权概率摇号暂不考虑。)
摇号软件用 .NET 开发,按照 《GB/T 10111-2008 随机数的产生及其在产品质量抽样检验中的应用程序》(以下简称《GB/T 10111-2008》)里的简单随机抽样算法进行摇号,伪代码如下:
Random r := new Random(6 位伪随机数种子);
while 摇号未完成 do
begin
repeat
n = r.Next(有效编码总数) + 1;
until 摇号基数编码 n 没被摇中;
摇出 n;
end;
从“缓解拥堵”网上下载到的摇号程序无法将摇号结果导出。 交通委使用的必是另外一个可导出结果的版本, 至于它还有没有别的功能我们不得而知。作者用 Lazarus 重写了摇号程序以导出结果。
这里引出本文要讨论的第一个问题:小客车摇号需要采用的标准是否真正适用?先看《GB/T 10111-2008》 的适用范围:
- 本标准规定了随机数的产生及利用随机数进行随机抽样的方法。
- 本标准适用于分立个体类产品质量抽样检验的随机样本的抽取,也可用于调查抽样中随机样本的抽取。
- 本标准不适于于散料类产品质量抽样检验的样本抽取。
小客车摇号在于选出一部分人赋予权利,而产品质量抽样检验或者调查抽样是为了窥一斑而知全貌,这是两个完全不同的问题,《GB/T 10111-2008》并不适用。
2. 不等概率抽样
摇号池确定以后,摇号结果只依赖随机数种子。因此,一个编号被摇中的概率为:
\[P = \frac{能摇到该编号的随机数种子个数}{1000000}\]这里,假定一百万个随机数种子等概出现。
简单随机抽样是不等概率抽样,即各编码的中签概率不同。以 2013 年第 12 期为例,有效编码 1811403 个, 中签指标 18211 个。遍历一百万个随机数种子, 统计各编号的中签次数可知,最少的中签 9616 次,最多的 10712 次。如果中签概率相等,则每编号的中签次数应为 10053.533。 也即在该期摇号池确实后,有些人“天生”地比别人惨,中签概率比标称概率低(最惨的低 4.4%); 有些人则“天生”地比别人幸运,最幸运的中签概率比标称概率高 6.5%。
自 2014 年开始的所谓加权概率摇号,$n$ 倍概率即将一个编码赋予 $n$ 个摇号基数编码。现有算法显然也无法保证得到 $n$ 倍概率的效果。 同样,一个家庭多人参加摇号,该家庭中签的概率也非简单的加倍关系。 鉴于一个家庭中多个申请人的编码在摇号池中的大小关系随机, 能保证简单的概率加倍关系的充要条件为:所有可能的摇号结果 ${N \choose M}$ 摇出概率相等。 这里摇号池中编码数为 $N$,指标数为 $M$,所有可能的摇号结果数即 $N$ 中选 $M$的组合数。${N \choose M}$ 是天文数字, 而在现在的摇号机制下,只有其中区区一百万种有摇出的可能。
“失之毫厘,谬以千里。” 公平者, 保障法律面前人人平等和机会均等,避免歧视对待。小客车摇号采用不等概抽样,不能保证申请人“机会均等”,显失公平。
3. 随机数种子的选取
摇号现场工作人员通过抓阄在现场随机找出 6 个人,通过按键的方法各选一位数。按键选数字的方法若不公正, 将直接颠覆简单随机抽样仅有的一点随机性。
看着现场工作人员一本正经地下令“开始摇号”、“刻盘”,稍稍一想,整个小客车摇号方案不过是个笑话罢了,认真不得。
4. 让数据讲话
自 2014 年 2 月 25 日起,摇号程序和摇号池编码文件已可下载,接下来本文试对数据做一点分析。
记第 $i$ 期摇号有效申请编码组成的集合为 $\Omega_i$,记第 $i$ 期中签编码组成的集合为 $\Omega_{i,win}$。
4.1 消失的编码
比较 $\Omega_i$ 与 $\Omega_{i+1}$,前者比后者多了一些元素:第 $i$ 期摇中的,以及其它“消失的编码”。我们将第 $i$ 期消失的编码记作 $\Omega_{gone,i+1}$,则有
\[\Omega_{gone,i+1}=\Omega_i - \Omega_{i+1} - \Omega_{win,i}\]$\Omega_{gone,i+1}$ 里的编码在第 $i$ 期并未中签,但也没参加下一次摇号。依理,这样编码应该不多,其实不然, 比如到 2012 年第 4 期时,有十八万余“老”编码没有参加此次摇号。主要原因是自 2012 年 1 月 1 日新的摇号细则将申请有效期改为三个月,申请人需要点击“确认延期”来延长有效期。
$\Omega_{gone,i+1}$ 在 $\Omega_i$ 中所占比重(元素数目之比)的曲线如下。
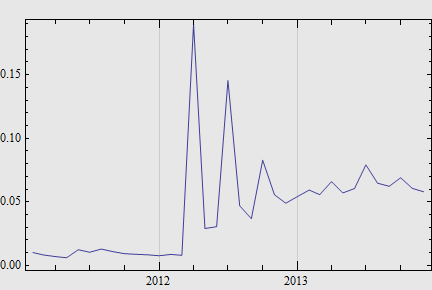
上图与欠阻尼振动曲线颇有几分相似。经过 11 个月,一众申请人方完成对新规定的消化吸收。这是一次很妙的社会行为实验。
4.2 真正消失的编码
$\Omega_{gone,i}$ 里的申请人在意识到忘记“确认延期”时,会尽快重新申请。把参加过后续摇号的编码从 $\Omega_{gone,i}$ 中删除,我们可以得到一个“真正”消失了的编码集合 $\Omega_{truly-gone,i}$:
\[\Omega_{truly-gone,i}=\{a | a \in \Omega_{gone,i} \land a \notin \Omega_{j = i + 1, \ldots}\}\]由于我们的数据只收集到 2013 年底,所以 2014 年后又参加摇号的编码没有从 $\Omega_{gone,i}$ 中删除,导致算出的 $\Omega_{truly-gone,i}$ 元素偏多,尤其是接近 2014 年时。
$\Omega_{truly-gone,i}$ 在 $\Omega_i$ 中所占比重的曲线图如下。如前所述,接近 2014 年时的几组 $\Omega_{truly-gone,i}$ 偏差较大,需略过不计。
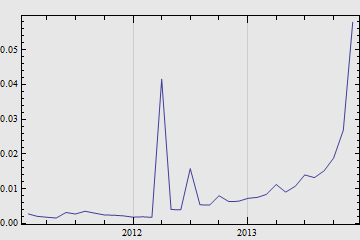
“有效期新政”同样将上面的曲线分成迥然不同的两段,着重分析 2012 年第 4 期之前的一段:每期未中签的编码里平均大约有 2.4‰退出了后续的摇号。退出原因大致有二:
-
指标需求已满足,比如家里其他人中签,通过其它途径获得指标等
-
指标需求消失,比如购车计划搁置,行为艺术等
4.3 孤独的编码
$\Omega_{truly-gone,i}$ 还有一个子集,这个集合里的编码只参加了一次摇号,未中签,然后便永远离开了,“挥一挥衣袖,不带走一片云彩”,我们称之为孤独编码,所组成的集合记作 $\Omega_{lonly,i}$:
\[\Omega_{lonly,i + 1}=\{a | a \in \Omega_i \land a \notin \Omega_{win,i} \land \left( \forall_{j \neq i}{a \notin \Omega_j}\right)\}\]如下图所示,$\Omega_{lonly,i}$ 的元素个数基本恒定(初始两个月除外)。
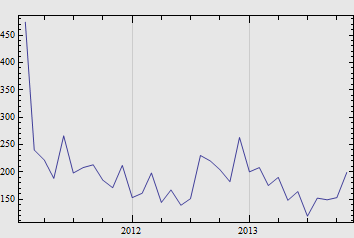
每期摇号,平均有 195 人是初次参加,未中签,然后离开。有效申请数从 18 万增加到 180 万,“孤独编码”数却几乎恒定不变,令人费解。 考虑到每期指标数也基本不变,或许这两者之间存在某种联系?
假如以最大的恶意去推测:存在一定量的计划外指标可以绕过摇号直接发给某些人,比如摇号指标数的 10%,这并不会让普通大众和权力人士惊诧。不妨大胆猜想这些计划外指标就在 200 个上下,也即摇号指标数的 1% 左右:200 个申请人的编码被修改,通过审核,参加当期摇号,然后直接赋予中签状态。
上述“方法”不需要控制伪随机数种子,还有一种需要加以控制以使指定编码中签的“方法”。遍历所有伪随机数种子,通过插入假编码调整指定编码的序号,使其中签,找到需要假编码最少的种子。假定有 2000000 有效编码,指标数 20000,则能选中 200 个指定编码的选法与总选法之比非常小,直接与这样的选法相对应的随机数种子几乎不可能存在:
\[{2000000 - 200 \choose 20000 - 200} / {2000000 \choose 20000} \widetilde= 3.72\times10^{-401}\]考虑允许插入大约 200 个假编码的情况。考察 $\Omega_{lonly,i + 1}$ 与 $\Omega_{win,i}$ 中相邻编码的关系,可以发现:两个中签编码“夹着”的“孤独编码”绝大部分只有一个,另有极少数两个的情况。插入一两个假编码所能增加的选法仍与 $10^{-401}$ 想去甚远,所以可以排除通过遍历寻找伪随机数种子的可能。
假如以最大的善意去推测: $\Omega_{lonly,i + 1}$ 里这些第 $i$ 新进加入的申请人,在第 $i$ 期摇号时,亲朋中签,需求得以满足。
在进一步讨论之前,我们先看每期新增编码的数目。
4.4 新增编码
某编码在第 $i$ 期首次参加摇号,则称该编码是该期的新增编码,中途退出又再次参加的不在此列,即
\[\Omega_{new,i}=\Omega_i - \Omega_{i-1} - \ldots - \Omega_1, i > 1\]各期新增编码数如下所示。
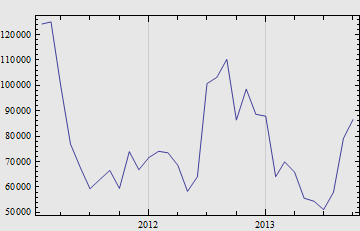
| $ | \Omega_{lonly} | $ 在 $ | \Omega_{new} | $、指标数中所占的比例,分别为 2.5‰、1% 左右: |
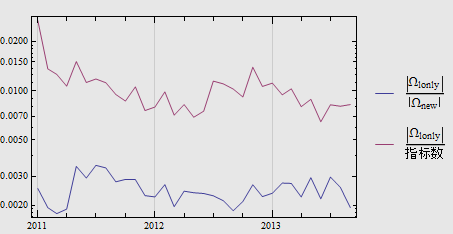
回到上面的假设, $\Omega_{new, i}$ 里有一部分申请人一旦亲朋中签,需求得以满足,便会退出摇号,可谓“但求一号”。这一部分人里的一部分“梦想成真”,构成集合 $\Omega_{lonly, i + 1}$,剩余部分仍会参加后续摇号。 粗略地,如果增加中签指标,但求一号族也会按比例进入 $\Omega_{lonly, i + 1}$。以 2013 年第 10 期为例,中签概率为 1.1%,可估得但求一号族在 $\Omega_{new, i}$ 中所占的比例大约为:
\[\frac{2.5‰}{1.1\%}=22.3\%\]这就是说,新增申请人中大约每四五个就有一个属于但求一号的情况。我们可以进行一个社会小调查,若此命题成立,则善意猜测成立;若不然,则恶意猜测成立,
5. 慌言
最后需要说明,本文里些许含混不清的结果很可能是对数据的刻意解读而得,不过是些“慌言”罢了,当不得真。
以《数学悖论奇景》里的一个例子作结。 某药物进行双盲实验。有研究人员随机取实验组 300 人,痊愈 200 人,无副作用;对照组 281 人,痊愈 187 人。显然,使用该药物可提高痊愈比例。 另有一组研究人员随机取实验组 870 人,痊愈 600 人,无副作用;对照组 886 人,痊愈 611 人。 结论同样为使用该药物可提高痊愈比例。 你的结论是什么?