Days ago I came across with some challenges. I wanted to have a try with answers in hand. Mathematica was my No.1 choice, but unfortunately could not be recognized by Pygments yet.
Almost trivial
A classic substitution cipher. At the first glance, it was so weirds, could it be Lewis Carroll’s “Jabberwocky”? “K towiekrp dwx” seemed to be a good breakthrough, since there are only two words that have only one letter, “a” and “I”. After some further try and error, I was defeated and turned to read the answer: K is O and it IS Jabberwocky.
Shouldn’t be very hard either
If you listen to it, you can find that it isn’t Morse code. Looking into its waveform, it seems that the carrier is modulated by a weak low frequency signal. Below is part of it:
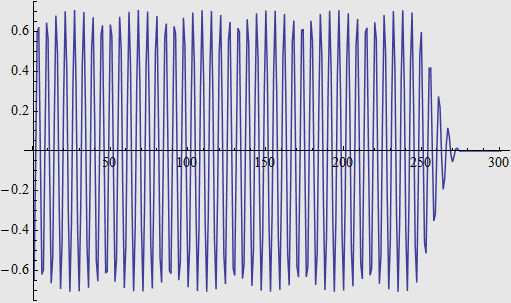
And the spectrum of the whole waveform, from which we could identify the carrier frequency is 1.3651kHz:
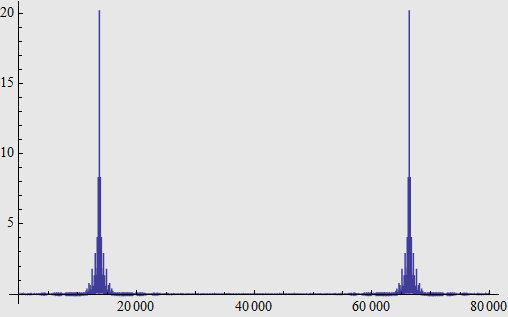
It is a narrow band signal. We could say that information is represented by the carrier itself, ON and OFF (a kind of amplitude-shift keying). Back to the answer, this is the Hellschreiber invented by Rudolf Hell nearly 100 years ago. There are tools to decode it, but I wanted to do it from scratch. Since this signal is very clean, to detect carrier’s existence, we can simply calculate a moving average using a moderate window size: Window size should not be too small, because we may get 0s during carrier ON; nor too large, because waveform length of a single bit (245 band, 14x14 pixels per letter) is limited. Then a down-sampling will give us the result. Note that we can surely use higher sampling rate such as 490 samples per second, then we get 28x28 pixels per letter.
wav = Import[...];
absAll = MovingAverage[Abs@wav[[1, 1, 1]], 10];
ListPlot[Take[absAll, {9980, 10400}], PlotRange -> All]
sampling[data_, dataTs_, Ts_] /; Ts > dataTs := Module[
{l},
l = Floor[Length[data] dataTs/Ts];
data[[1 + Round[Range[0, l - 1] Ts/dataTs]]]
];
MatrixPlot[(Rest /@ #)~Join~(Most /@ #) &@
Transpose@(Reverse /@
Partition[sampling[absAll, 1/8000, 1/245], 14]),
MaxPlotPoints -> Infinity]
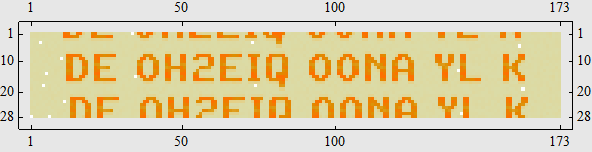
Actually, this can be decoded by a single line of code:
MatrixPlot[#~Join~# &@
Transpose[Reverse /@ Partition[wav[[1, 1, 1]], 230]],
AspectRatio -> 0.15, MaxPlotPoints -> Infinity]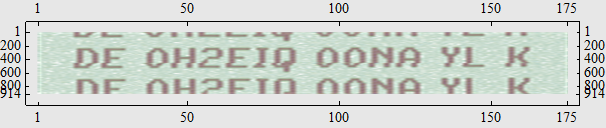
Might take some effort
Split this image into two halves, then either ImageSubtract or ImageAdd can be used to uncover the secret.
NSA-grade
I made an implementation of the Playfair cipher as follows.
shrink[s_String] :=
Characters@
StringReplace[ToUpperCase@s, {" " -> "", "\t" -> "", "J" -> "I"}];
prepare[{c1_, c2_, ls___}, acc_] /; c1 != c2 :=
prepare[{ls}, Append[acc, {c1, c2}]];
prepare[{c1_, c2_, ls___}, acc_] /; c1 == c2 :=
prepare[{c2, ls}, Append[acc, {c1, "X"}]];
prepare[{c1_}, acc_] := Append[acc, {c1, "X"}];
prepare[{}, acc_] := acc;
prepare[s_String] := prepare[shrink@s, {}];
initkey[k_String] :=
Partition[
DeleteCases[
DeleteDuplicates[shrink@k~Join~CharacterRange["A", "Z"]], "J"], 5];
codepair[{c1_, c2_}, key_, Dir_] := Module[
{x1, y1, x2, y2},
{x1, y1} = First@Position[key, c1];
{x2, y2} = First@Position[key, c2];
Which[x1 == x2, {key[[x1, Mod[y1 - 2 Dir, 5] + 1]],
key[[x1, Mod[y2 - 2 Dir, 5] + 1]]},
y1 == y2, {key[[Mod[x1 - 2 Dir, 5] + 1, y1]],
key[[Mod[x2 - 2 Dir, 5] + 1, y1]]},
True, {key[[x1, y2]], key[[x2, y1]]}
]
];
encodepair[{c1_, c2_}, key_] := codepair[{c1, c2}, key, 0];
decodepair[{c1_, c2_}, key_] := codepair[{c1, c2}, key, 1];
PlayfairEncode[key_, s_] :=
StringJoin @@ (Flatten@encodepair[#, initkey@key] & /@ (prepare@s));
PlayfairDecode[key_, s_] :=
StringJoin @@ (Flatten@decodepair[#, initkey@key] & /@
Partition[shrink@s, 2]);
Output of PlayfairDecode was hard to read, so I wanted to segment a sentence into words automatically. Word segmentation is not a trial problem, which needs lots of prior information. Still, I wrote a naive word segment function like this:
- first create a graph
- then use FindShortestPath to select the best segmentation.
Here, each letter was represented by a vertex. Each edge connected the start of a word candidate to the start of the next one. If this word candidate exists in our dictionary, the longer the candidate, the smaller the edge weight; if not, the longer the candidate, the larger the weight. Longer words were preferred, and adjacent not-exist word would be combined into a larger one thanks to the use of Sqrt which grows slower than linear functions.
segment[str_String] := Module[
{lst, edges, weights, i, j, s, p, g, t},
s = ToLowerCase@str;
lst = Characters@s;
t = Flatten[Table[{i, j}, {i, 1, Length@lst}, {j, i, Length@lst}],
1];
edges = First@# \[DirectedEdge] Last@# + 1 & /@ t;
weights =
If[DictionaryLookup[StringTake[s, #], IgnoreCase -> True] != {},
1/(Last@# + 1 - First@#), Sqrt[1.2 (Last@# + 1 - First@#)]] & /@
t;
g = Graph[edges, EdgeWeight -> weights];
p = FindShortestPath[g, 1, Length@lst + 1];
StringTake[s, {First@#, Last@# - 1}] & /@ Partition[p, 2, 1]
];
In[3] := segment["THISISMYOLDFRIENDMONSIEURPOIROTWHOMIHAVENOTSEENFORYEARS"]
Out[3] = {"this", "is", "my", "old", "friend", "monsieur", "poirot", "who",
"mi", "have", "not", "seen", "for", "years"}
A problem I had encountered here was that my Mathematica (9.0 released last year) could not handle EdgeWeight specified in Property, while newer versions should be OK.
Here came the end of this wonderful journey. Thank Oona for making it.
N
X F
C R L
E M S G
O Y G C D
L H B N F D
R H F N F T A
D R K C S L P L
U H T G O L D A X